市西初级中学2019学年第一学期期中初二数学试题
1、选择题(本大题共6题,每题3分,满分18分)【每题只有一个正确选项,在答卷纸相应地方填涂】
1.下列等式未必成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列二次根式中,最简二次根式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列等式成立的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.已知命题“关于![]() 的一元二次方程
的一元二次方程![]() ,当
,当![]() 时必有实数解”,能说明这个命题是假命题的一个反例可以是( )
时必有实数解”,能说明这个命题是假命题的一个反例可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知三角形两边长分别是![]() 和2,第三边的长为
和2,第三边的长为![]() 的根,则这个三角形的周长是( )
的根,则这个三角形的周长是( )
A.4 B.![]() C.
C.![]() D.没有
D.没有
6.下列命题中,是真命题的是( )
A.假如![]() ,那样
,那样![]() ;
;
B.有两边及第三边上的高对应相等的两个三角形全等;
C.两个三角形全等,它们的周长肯定相等;
D.周长相等的两个三角形全等.
2、填空题(本大题共12题,每题3分,满分36分)
【请将结果直接填入答卷纸的相应地方上】
7.二次根式![]() 中,
中,![]() 的取值范围是___________.
的取值范围是___________.
8.假如最简二次根式![]() 和
和![]() 是相同种类二次根式,那样
是相同种类二次根式,那样![]() __________.
__________.
9.分母有理化:![]() __________.
__________.
10.不等式![]() 的解集是__________.
的解集是__________.
11.化简求值:当![]() 时,二次根式
时,二次根式![]() 的值为___________.
的值为___________.
12.在实数范围内因式分解:![]() ________.
________.
13.如图,在面积为![]() 正方形
正方形![]() 中,点
中,点![]() 在
在![]() 上,且
上,且![]() 的面积为
的面积为![]() ,则
,则![]() 的长为_______.(用含有
的长为_______.(用含有![]() 的代数式表示)
的代数式表示)

14.若关于![]() 的方程
的方程![]() 有实数根,则
有实数根,则![]() 的取值范围是___________.
的取值范围是___________.
15.将命题“关于某直线对称的两个三角形全等”,改写成“假如…,那样…”的形式:
假如___________________________,那样________________________.
16.已知![]() 、
、![]() 为实数,且
为实数,且![]() ,则
,则![]() 的值为________.
的值为________.
17.已知![]() ,则
,则![]() __________.
__________.
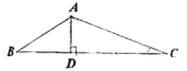
18.如图,在![]() 中,
中,![]() ,
,![]() 于
于![]() ,且
,且![]() ,那样
,那样![]() 的度数是__________.
的度数是__________.
3、解答卷(本大题共8题,满分66分)【将下列各题的解答过程,做在答卷纸上】
19.先化简,再求值:已知![]() ,求
,求![]() 的值.
的值.
20.(1)计算:![]() ;
;
(2)计算:![]() .
.
21.(1)在实数范围内因式分解:![]() .
.
(2)解关于![]() 的方程:
的方程:![]() (
(![]() 是已知数).
是已知数).
22.已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)假如方程的根的辨别式的值为4,求![]() 的值;
的值;
(2)![]() 取何值时,方程有两个相等的实数根,并求出这两个根.
取何值时,方程有两个相等的实数根,并求出这两个根.
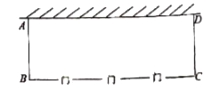
23.某建筑工程队,在工地一边的靠墙处(墙长60米),用124米长的建筑材料围成一个占地面积为2010平米的长方形仓库(图中的长方形![]() ),为了便于在紧急状况下搬运货物,现决定在与墙平行的边
),为了便于在紧急状况下搬运货物,现决定在与墙平行的边![]() 上预留出3个长度为1米的门,求与墙垂直的边
上预留出3个长度为1米的门,求与墙垂直的边![]() 的长.
的长.
24.阅读理解:小明同学进入初中二年级将来,念书越发认真.
在学习“用因式分解法解方程”时,课后习题中有如此一个问题:
下列方程的解法对不对?为何?![]()
解:![]() 或
或![]() .
.
解得![]() 或
或![]() .
.
所以![]() ,
,![]() .
.
同学们都觉得不对,缘由:有些说该题的因式分解是不对的;有些说将答案代入方程,方程左右两边不成立,等等.
小明同学除去觉得该解法不正确,还给出了一种因式分解的做法,小明同学的做法如下:
取![]() 与
与![]() 的平均值
的平均值![]() ,马上
,马上![]() 与
与![]() 相加再除以2.
相加再除以2.
那样原方程可化为![]() .
.
左侧用平方差公式可化为![]() .
.
再移项,开平方可得![]()
请你认真阅读小明同学的办法,并用这个办法推导:
关于![]() 的方程
的方程![]() 的求根公式(此时
的求根公式(此时![]() ).
).
25.求证:等腰三角形腰上的高与底边的夹角等于其顶角的一半.
(1)在图中根据下面“已知”的需要,画出符合题意的图形,并依据题设和结论,结合图形,用符号语言写出“求证”.
已知:在![]() 中,
中,![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
求证:_____________________________________________________.
(2)证明上述命题:
26.已知:在![]() 中,
中,![]() ,
,![]() 的高
的高![]() 、
、![]() 交于点
交于点![]() .
.
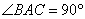
(1)求证:![]() .
.
(2)过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,求证:
,求证:![]() .
.
27.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 所在的直线上运动,作
所在的直线上运动,作![]() (
(![]() 、
、![]() 、
、![]() 按逆时针方向).
按逆时针方向).

(1)如图①,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 交
交![]() 于
于![]() .
.
①求证:![]() .
.
②当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的长.
的长.
(2)如图②,当点![]() 在
在![]() 的延长线上运动,
的延长线上运动,![]() 的反向延长线与
的反向延长线与![]() 的延长线相交于点
的延长线相交于点![]() ,是不是存在点
,是不是存在点![]() ,使
,使![]() 是等腰三角形?若存在,写出点
是等腰三角形?若存在,写出点![]() 的地方;若没有,请简要说明理由.
的地方;若没有,请简要说明理由.







